มูลค่าของเงินตามระยะเวลา


คำสำคัญ : มูลค่าของเงินตามระยะเวลา, มูลค่าในอนาคต, มูลค่าปัจจุบัน
Abstract
This article is a documentary study by collecting data from textbooks and research paper related to analytical instruments using the time value method, which the objective for investors or financial analysts, organization executives and those who are interested understand the importance, meaning, benefits and necessity of time value of money. To lead to appropriate financial decisions that benefit the stakeholders both directly and indirectly. The term value of money can be divided into two categories: (1) future value is the amount of money in the future resulting from an increase in the value of capital over a period of time with compound interest. And (2) present value is a future amount that is discounted at a discount rate to convert back to present value.
Keywords : Time value of money, Future value, Present value,
บทนำ
การบริหารจัดการการเงินเป็นอีกในหนึ่งส่วนสำคัญที่จะทำให้ธุรกิจเกิดกำไร และมีเงินในการหมุนเวียนกิจการและทำให้ธุรกิจสามารถบริหารจัดการการเงินได้อย่างมีประสิทธิภาพ ซึ่งจะสามารถใช้ประโยชน์จากมูลค่าของเงินได้อย่างเต็มที่ (PeerPower, 2562) โดยในชีวิตของคนเราทุกคนย่อมต้องมีการตัดสินใจทางการเงิน ไม่ว่าจะเป็นการตัดสินใจเพื่อตัวเองหรือเพื่ออนาคตของครอบครัว เช่น การตัดสินใจฝากเงิน การตัดสินใจลงทุน การตัดสินใจกู้เงิน หรือการซื้อบ้านซื้อรถ แต่ในเมื่อไม่ว่าการฝากเงินหรือการกู้เงินก็ต้องมีปัจจัยเรื่องระยะเวลา ดอกเบี้ย หรือแม้กระทั่งอัตราเงินเฟ้อเข้ามาเกี่ยวข้อง ซึ่งจะทำให้เงิน 1 บาท มีมูลค่าแตกต่างกันไปในแต่ละช่วงเวลา การประเมินผลกระทบของเงินต่อสถานะการเงินและตัดสินใจได้อย่างเหมาะสมจึงไม่อาจทำได้ด้วยการดูจากตัวเลขที่ปรากฏ แต่ต้องคำนวณถึงมูลค่าที่แท้จริงของเงินนั้นๆ ด้วย (ไทยพับลิก้า, 2561) ซึ่งในทางการเงิน หลักการที่ช่วยให้เห็นผลกระทบที่แท้จริงของตัวเงินที่เข้ามาหรือออกไปในระยะเวลาต่างๆ เรียกว่า มูลค่าเงินตามเวลา หรือ Time value of money
ในยามที่คนต้องการบริโภคและลงทุนเพิ่มมากขึ้น ซึ่งส่งผลให้ราคาสินค้าและบริการปรับสูงขึ้น แต่ถ้ารายได้ยังคงเดิมจะทำให้คนซื้อของได้น้อยลงและกระทบต่อชีวิตความเป็นอยู่ ธนาคารแห่งประเทศไทยจึงมีหน้าที่หลักในการดูแลเสถียรภาพด้านราคา โดยใช้อัตราดอกเบี้ยนโยบายเป็นเครื่องมือในการดำเนินนโยบายการเงิน ทั้งนี้ เมื่อเงินเฟ้อเพิ่มสูงขึ้นก็จะทำให้ต้องมีการปรับขึ้นอัตราดอกเบี้ยนโยบายเพื่อส่งสัญญาณให้ธนาคารพาณิชย์รู้ว่าธนาคารแห่งประเทศไทยต้องการให้อัตราดอกเบี้ยในตลาดการเงินปรับสูงขึ้น โดยธนาคารแห่งประเทศไทยจะดูดซับสภาพคล่องหรือดูดเงินออกจากระบบการเงินเพื่อให้ภาวะการเงินตึงตัว ดังนั้น ธนาคารพาณิชย์แต่ละแห่งจะต้องเพิ่มสภาพคล่องของตนเอง โดยการปรับอัตราดอกเบี้ยเงินฝากให้สูงขึ้นเพื่อระดมเงินฝากมากขึ้น ขณะเดียวกันก็ปรับเพิ่มอัตราดอกเบี้ยเงินกู้ตามต้นทุนเงินฝากที่สูงขึ้น การที่อัตราดอกเบี้ยเงินฝากสูงขึ้นจะจูงใจให้คนมาฝากเงินมากขึ้นและใช้จ่ายน้อยลง ขณะที่อัตราดอกเบี้ยเงินกู้ที่สูงขึ้นก็ทำให้คนกู้เงินน้อยลง เมื่อความต้องการสินค้าและบริการลดลงจะส่งผลให้ระดับราคาสินค้าลดลง และชะลอเงินเฟ้อ ในทางกลับกัน หากเศรษฐกิจซบเซา ประชาชนจะไม่อยากใช้จ่าย ราคาสินค้าและบริการก็จะปรับลดลงและทำให้ต้องปรับลดอัตราดอกเบี้ยนโยบายลงเพื่อกระตุ้นเศรษฐกิจ การที่อัตราดอกเบี้ยนโยบายลดลงจะทำให้อัตราดอกเบี้ยอ้างอิงของธนาคารพาณิชย์ลดลงเช่นกัน ซึ่งเป็นแรงจูงใจให้คนบริโภคและลงทุนมากขึ้น เมื่อความต้องการสินค้าและบริการเพิ่มสูงขึ้นจะส่งผลให้ระดับราคาปรับสูงขึ้นตามไปด้วย (ธนาคารแห่งประเทศไทย, 2557)
ในระบบเศรษฐกิจนั้นจะเห็นได้ว่า เวลาเป็นปัจจัยอย่างหนึ่งในการกำหนดมูลค่าของเงิน ซึ่งเป็นที่ยอมรับกันมานานแล้ว เงินจะมีค่าเปลี่ยนแปลงไปตามระยะเวลา กล่าวคือเมื่อเวลาเปลี่ยนแปลงไปค่าของเงินจะเปลี่ยนตามไปด้วย ฉะนั้นเงินที่มีอยู่ในขณะนี้ย่อมมีค่ามากกว่าเงินจำนวนเท่ากันในเวลาอีกหนึ่งปีข้างหน้า ดังนั้นเราจะสามารถเปรียบเทียบค่าของเงินในระยะเวลาที่ต่างกันได้โดยทำให้ค่าเงินของเงินในอนาคตมาเป็นค่าปัจจุบันได้ด้วยวิธีหามูลค่าปัจจุบัน ซึ่งนอกจากนั้นอัตราดอกเบี้ยหรืออัตราส่วนลด ก็ยังเป็นปัจจัยสำคัญที่จะทำให้เกิดความแตกต่างในค่าของเงิน (อรุณรุ่ง วงศ์กังวาน, 2557) จากงานวิจัยของ Sarker และ Pan (1994) ได้ศึกษาเกี่ยวกับผลกระทบของเงินเฟ้อและมูลค่าเงินตามเวลาต่อปริมาณการสั่งซื้อและการขาดแคลนที่อนุญาต พบว่า ปริมาณการสั่งซื้อที่เหมาะสมและการขาดแคลนสูงสุดที่อนุญาตนั้นแตกต่างกันไปตามความแตกต่างระหว่างอัตราเงินเฟ้อและส่วนลดเวลา ซึ่งผลการคำนวณระบุว่าผลกระทบต่อระบบมีนัยสำคัญมากขึ้นเมื่อความแตกต่างระหว่างอัตราเงินเฟ้อและอัตราคิดลดด้านเวลาเพิ่มขึ้น และจากงานวิจัยของ ศิรประภา ศรีวิโรจน์, ลักขณา ลุสวัสดิ์ และ ธตรฐ จำรูญกุล (2563) ได้ศึกษาเกี่ยวกับการประเมินโครงการลงทุนด้วยเครื่องมือวิเคราะห์ทางเศรษฐศาสตร์ พบว่า โครงการลงทุนเป็นโครงการที่ก่อให้เกิดการพัฒนาด้านต่างๆ ซึ่งก่อให้เกิดการขับเคลื่อนทางเศรษฐกิจและสังคม ซึ่งการประเมินโครงการและการพิจารณาตัดสินใจเลือกลงทุนหรือชะลอการลงทุนย่อมต้องมีผลกระทบต่อสังคมและเศรษฐกิจ โครงการภาครัฐอย่างน้อยควรนำเครื่องมือเทคนิคพื้นฐานไปวิเคราะห์การลงทุน สำหรับโครงการลงทุนของภาคเอกชนอาจนำเครื่องมือเทคนิคอื่นวิเคราะห์อื่นร่วมได้ หรือหากเป็นโครงการลงทุนของภาคเอกชนขนาดเล็กสามารถเปลี่ยนจากวิธีมูลค่าปัจจุบันแบบเดิม เป็นวิธีมูลค่าปัจจุบันสุทธิสำหรับกิจการขนาดเล็กได้ แต่อย่างไรก็ดีการเลือกใช้เครื่องมือเทคนิคต้องให้สอดคล้องเหมาะสมกับข้อมูลของโครงการที่จะนำมาพิจารณา ดังนั้นการนำเครื่องมือหรือเทคนิควิธีไปใช้ในการประเมินเพื่อพิจารณาตัดสินใจลงทุนในโครงการควรต้องศึกษาข้อมูลที่เกี่ยวข้องประกอบการตัดสินใจให้มากที่สุด ทั้งนี้เพื่อสามารถได้ข้อสรุปนำไปสู่การตัดสินใจที่เป็นประโยชน์สูงสุดแก่นักลงทุนและสังคมโดยรวม
วัตถุประสงค์
1. เพื่อให้นักลงทุนหรือนักวิเคราะห์ทางการเงิน ผู้บริหารองค์กร ได้เข้าใจถึงความสำคัญและความหมายของมูลค่าของเงินตามระยะเวลา
2. เพื่อให้นักลงทุนหรือนักวิเคราะห์ทางการเงิน ผู้บริหารองค์กร ได้เข้าใจถึงประโยชน์และความจำเป็นของมูลค่าของเงินตามระยะเวลา
เนื้อหาของบทความ (บทวิเคราะห์เกี่ยวกับ แนวคิด ทฤษฎี ผลงานวิจัย ประเด็นสำคัญ ข้อดีหรือประโยชน์)
แนวคิดเกี่ยวกับมูลค่าของเงินตามระยะเวลา
จุดเริ่มต้นของแนวคิดเรื่อง มูลค่าของเงินตามระยะเวลา (Time value of money: TVM) เกิดขึ้นจากนักลงทุนกลุ่มหนึ่งที่มีความคิดอยากที่จะได้เงินทันทีตอนนี้หรือในปัจจุบันมากกว่าที่จะต้องรอรับเงินในจำนวนที่เท่ากันในอนาคต สาเหตุที่เป็นเช่นนั้น เพราะว่าเงินนั้นมีความสามารถที่จะเติบโตหรือเพิ่มมูลค่าขึ้นได้เมื่อเวลาผ่านไป ยกตัวอย่างเช่น เมื่อฝากเงินเข้าบัญชีธนาคารก็จะได้รับดอกเบี้ยจากการฝากเงิน ดอกเบี้ยที่ได้นี้ถือเป็นมูลค่าอย่างหนึ่งที่เกิดขึ้นจากระยะเวลาที่ผ่านไป หรือสมมติว่ามี 2 ทางเลือกระหว่าง รับเงิน 30,000 บาท ตอนนี้กับรับเงิน 30,000 บาท ในอีก 1 ปีข้างหน้า แน่นอนว่าคนส่วนใหญ่นั้นก็จะต้องเลือกทางเลือกที่ 1 และรับเงินในวันนี้ นั่นก็เพราะว่ามูลค่าของเงิน 30,000 บาท ในปัจจุบันนั้นมีมูลค่าหรือมีความสามารถในการทำประโยชน์ได้มากกว่าในอนาคต หรือที่เรียกว่า ค่าเสียโอกาส (Opportunity Costs) ซึ่งค่าเสียโอกาสนี้ไม่ได้หมายความถึงแค่ค่าเสียเวลาที่เราต้องรอในระยะเวลา 1 ปีเพื่อให้ได้รับเงินจำนวนเท่าเดิม แต่ยังรวมถึงโอกาสต่างๆ ที่จะสามารถนำเงินก้อนนี้ไปบริหารหรือทำประโยชน์อื่นๆ ได้อีก หรือจะกล่าวคือ มูลค่าของเงินตามระยะเวลา คือ มูลค่าของเงินเมื่อเวลาผ่านไป ซึ่งเป็นอีกหนึ่งแนวคิดที่มองเห็นว่าคุณค่าของเงินในปัจจุบันนั้นอาจจะถูกลดทอนค่าเงินลงเมื่อเวลาผ่านไป (PeerPower, 2562)
มูลค่าของเงินตามระยะเวลา หรือ Time value of money (TVM) ถือเป็นหลักการพื้นฐานเบื้องต้นของทฤษฎีการเงิน ซึ่งมีความหมายของคํานี้ตามชื่อ คือ เงิน ณ เวลาที่แตกต่างกันมีมูลค่าที่ไม่เท่ากัน เป็นแนวคิดเรื่องมูลค่าของเงินตามระยะเวลาซึ่งจะช่วยให้สามารถเปรียบเทียบมูลค่าของเงินในเวลาที่แตกต่างกันได้อย่างเหมาะสม (MONEY BUFFALO, 2563) มูลค่าของเงินตามระยะเวลาเป็นแนวคิดเกี่ยวกับเงินที่ได้รับในวันนี้มีมูลค่าน้อยกว่าเงินที่จะได้รับในอนาคต เพราะสามารถสร้างผลตอบแทนได้จาก เงินที่ได้รับในวันนี้ (อัจฉรา โยมสินธุ์, 2555) ซึ่งสามารถแบ่งประเภทของมูลค่าของเงินตามระยะเวลาออกได้เป็น 2 ประเภท ได้แก่ มูลค่าในอนาคต (Future Value) และมูลค่าปัจจุบัน (Present value)
1. มูลค่าในอนาคต (Future Value: FV)
มูลค่าในอนาคต (Future value: FV) คือ มูลค่าของเงินที่เปลี่ยนแปลงไปตามระยะเวลา (Time) และอัตราผลตอบแทน (Rate of return) ที่ได้รับ ซึ่งมูลค่าในอนาคต (Future value: FV) คือ มูลค่ารวมของเงินต้น (มูลค่าปัจจุบัน) กับผลตอบแทนที่เกิดขึ้นในช่วงเวลาหนึ่ง (อัจฉรา โยมสินธุ์, 2555) โดยการคิดหามูลค่าในอนาคตหรือมูลค่าของเงินที่เสียไปนั้นมีปัจจัยหลายอย่างที่เป็นตัวกำหนด เช่น การคิดดอกเบี้ยแบบรายปีหรือรายเดือน สูตรการหาโดยทั่วไปนั้นจะไม่ได้มีปัจจัยที่หลากหลายเหมือนในชีวิตจริง แต่ก็มีหลายคนที่นำสูตรนี้ไปประยุกต์ใช้กับการทำบัญชีหรืองบประมาณจริงๆ ซึ่งตัวแทนที่จะสามารถบอกได้ว่า หากต้องการเลือกที่จะรับเงินในอนาคตแทนเงินก้อนในปัจจุบันนั้นควรจะมีค่าเท่าไหร่ ค่าที่จะเป็นตัวชดเชยนั่นตามทฤษฎีจะเรียกว่า อัตราผลตอบแทนหรืออัตราคิดลด ซึ่งจะเป็นตัวแทนของทั้งอัตราเงินเฟ้อ ผลตอบแทนที่ต้องการ หรืออัตราดอกเบี้ยทั้งหมดนี้ขึ้นอยู่กับความต้องการของผู้คํานวณ (MONEY BUFFALO, 2563) หากสมมติว่า ปัจจุบันมีเงิน 10,000 บาท และนำเอาเงิน 10,000 บาท นั้นไปฝากธนาคาร เมื่อเวลาผ่านไป 2 ปี จำนวนเงินที่ต้องได้กลับมาย่อมมากกว่า 10,000 บาท เหตุผลเนื่องจากธนาคารจะให้ดอกเบี้ย ซึ่งดอกเบี้ยที่ได้รับก็จะทดแทนทั้งการรอคอยการบริโภคหรือเงินเฟ้อที่อาจจะเกิดขึ้น ซึ่งรวมไปถึงความเสี่ยงที่อาจจะไม่ได้เงิน แปลว่า หากต้องการเลื่อนรับเงินจากวันนี้ไปเป็นวันข้างหน้า โดยเลือกที่จะไม่รับเงิน 10,000 บาท ณ วันนี้ วันข้างหน้าก็จะได้รับเงินมากกว่า 10,000 บาท
สำหรับการคำนวณหามูลค่าของเงินในอนาคตสามารถคำนวณได้จากการแทนค่าตัวแปรลงในสมการการสามารถคำนวณมูลค่าของเงินในอนาคต (Future value: FV) ได้ดังนี้
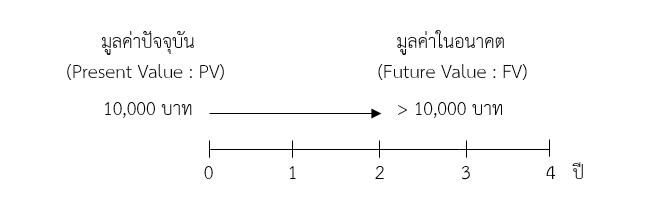
มูลค่าในอนาคต = มูลค่าปัจจุบัน x (1 + อัตราผลตอบแทน)ระยะเวลา
FV = PV x [1 + (i/n)]n*t
เมื่อ FV = มูลค่าเงินในอนาคต
PV = มูลค่าปัจจุบัน
i = อัตราผลตอบแทน (Rate of return)
n = จำนวนงวด
t = จำนวนระยะเวลา
ตัวอย่างที่ 1 สมมติว่ามูลค่า ณ เวลาปัจจุบัน (PV) เท่ากับ 100 บาท และมีอัตราผลตอบแทนเท่ากับ 2% ต่อปี ซึ่งเมื่อเวลาผ่านไปอีก 2 ปีข้างหน้า มูลค่าในอนาคตของเงิน 100 บาท ควรจะมีมูลค่าเป็นจำนวนเงินเท่าไหร่ โดยจะสามารถเขียนเป็นเส้นเวลาได้ตามภาพเส้นเวลาด้านล่าง
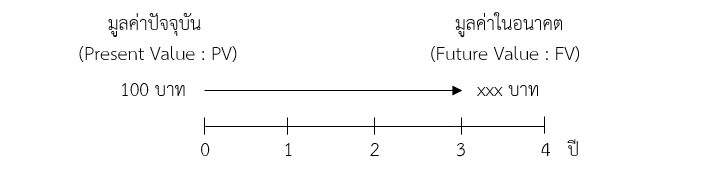
ดังนั้น ในอีก 2 ปีข้างหน้า มูลค่าในอนาคตของเงิน 100 บาท ควรจะมีมูลค่าเท่ากับ 100 x [1 + (0.02/1)]3*1 เท่ากับ 106.12 บาท ซึ่งสามารถแยกคำนวณทีละปีได้ดังนี้
ปีที่ 1; FV = 100.00 x (1 + 0.02)1 = 102.00 บาท
ปีที่ 2; FV = 102.00 x (1 + 0.02)1 = 104.04 บาท
ปีที่ 3; FV = 104.04 x (1 + 0.02)1 = 106.12 บาท
จะเห็นว่าเงินต้นปีที่ 2 จำนวน 102 บาท มีผลตอบแทนของปีที่ 1 รวมอยู่ด้วย 2 บาท ผลตอบแทนที่ได้รับในปีที่ 2 จึงมากกว่าปีแรก (2.04 บาทเมื่อเทียบกับดอกเบี้ยปีแรก 2 บาท) แสดงว่าจะได้รับผลตอบแทนจากดอกเบี้ยหรือที่เรียกว่า ดอกเบี้ยทบต้น (Compound interest) โดยดอกเบี้ยแบบทบต้น คือ การนำดอกเบี้ยที่ได้รับจากการฝากเงินแต่ละงวดมารวมเป็นเงินต้นของงวดต่อๆ ไป ซึ่งผลของดอกเบี้ยทบต้นนี้จะทำให้ดอกเบี้ยที่ได้รับในงวดต่อๆ ไปเพิ่มขึ้นเรื่อยๆ มูลค่าของเงินที่เพิ่มตามเวลายิ่งโตมากขึ้น เพราะได้ดอกเบี้ยบนดอกเบี้ยอีกชั้นหนึ่ง (ไทยพับลิก้า, 2561)
ตัวอย่างที่ 2 ปัจจุบันมีเงิน 1,000,000 บาท และนำไปลงทุนซึ่งจะได้ผลตอบแทน 4% ในอีก 1 ปีข้างหน้าควรจะมีมูลค่าเป็นจำนวนเงินเท่าไหร่ โดยจะสามารถเขียนเป็นเส้นเวลาได้ตามภาพเส้นเวลาด้านล่าง

ดังนั้น ในอีก 1 ปีข้างหน้าจะได้รับเงินทั้งสิ้น 1,040,000 บาท โดยจะเห็นได้ว่า เงินจำนวน 1,000,000 บาท มีมูลค่าในอนาคต (FV) เท่ากับ 1,000,000 x [1 + (0.04/1)]1*1 เท่ากับ 1,040,000 บาท หรือเงินจำนวน 1,040,000 บาท ในอีก 1 ปีข้างหน้าจะมีมูลค่าปัจจุบัน (PV) เท่ากับ 1,000,000 บาท
นอกจากนี้ มูลค่าของเงินตามระยะเวลายังสามารถมองในมุมกลับได้เช่นกัน เช่น เมื่อพบโปรโมชั่นจ่ายเงินสดลด 3% หรือเลือกที่จะจ่ายผ่านบัตรเครดิต ก็จะสามารถชำระเงินหลังจากนั้นได้สูงสุดถึง 55 วัน ประโยชน์จากการจ่ายด้วยเงินสด หรือประโยชน์จากการชำระบัตรเครดิตนั้นก็ถือมูลค่าของเงินตามระยะเวลาด้วยกันทั้งนั้น (PeerPower, 2562) ซึ่งจะเห็นได้ว่าเมื่อเงินเดินทางผ่านกาลเวลา มูลค่าของเงินก็จะมีค่าเปลี่ยนแปลงไป ถ้าเดินทางไปในอนาคตมูลค่าก็ควรจะเพิ่มขึ้น แต่ถ้าคิดคํานวณย้อนกลับ เช่น หากรู้ว่าจะได้เงินในอนาคตอีก 3 ปีข้างหน้าเป็นจำนวนเงิน 1,000,000 บาท แล้วคิดกลับมาเป็นมูลค่า ณ เวลาปัจจุบัน แน่นอนว่ามูลค่าเงินย่อมมีค่าน้อยกว่า 1,000,000 บาท แน่นอน แต่จะมีมูลค่าเท่าไหร่นั้นก็ขึ้นอยู่กับว่าอัตราคิดลดมีค่าเป็นเท่าไหร่
2. มูลค่าปัจจุบัน (Present value: PV)
มูลค่าปัจจุบัน (Present value: PV) คือ มูลค่า ณ วันนี้ของเงินจำนวนหนึ่งที่จะได้รับในอนาคต ซึ่งมูลค่าปัจจุบันของเงินในอนาคตภายใต้ช่วงเวลาและอัตราผลตอบแทนที่ได้กำหนดไว้ โดยมีหลักแนวคิดว่าเงินในปัจจุบันมีค่ามากกว่าเงินในอนาคต เช่น เงิน 1,000,000 บาท ในวันนี้จะมีค่ามากกว่า 1,000,000 บาทในอีกหลายปีข้างหน้า เหตุผลก็คือเงินในวันนี้สามารถนำไปลงทุนได้เลยทันที ซึ่งจะสร้างผลตอบแทนที่เพิ่มขึ้นมา เงินในปัจจุบันจึงมีมูลค่ามากกว่าเงินในอนาคต (myAccount, 2561) ซึ่งจะเป็นวิธีการคํานวณเพื่อหาว่าถ้าหากต้องการมีเงินจำนวนหนึ่งในอนาคตจะต้องมีเงินต้นเท่าไหร่ในปัจจุบันจึงจะสามารถมีเงินจำนวนดังกล่าวได้ภายในระยะเวลาที่กำหนด หรือก็คือ การคํานวณหาเงินต้นที่ต้องใช้ลงทุนนั่นเอง (K. Pair, 2561) มูลค่าปัจจุบันจึงเป็นหัวข้อที่มีความสำคัญมากในวิชาการเงิน โดยหากสมมติว่า ต้องการเก็บเงินให้ได้ 10,000 บาทภายในระยะเวลา 2 ปี โดยจะนำเงินต้นไปลงทุนในการลงทุนที่ให้ผลตอบแทนแน่นอน ซึ่งการคํานวณหาเงินต้นที่ต้องใช้ลงทุนหรือการคำนวณหามูลค่าปัจจุบันนั้นจะทำให้ทราบว่าต้องนำเงินต้นไปลงทุนในปีแรกเป็นจำนวนเงินเท่าไหร่ถึงจะได้รับเงิน 10,000 บาทในอีก 2 ปีข้างหน้า
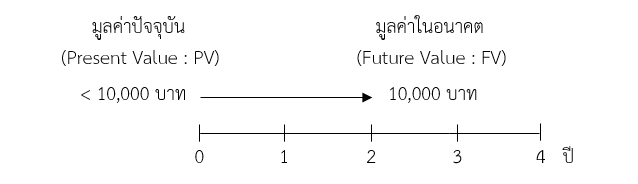
สำหรับการคำนวณหามูลค่าปัจจุบันหรือที่เป็นเงินต้นที่ต้องใช้ในการลงทุน สามารถคำนวณได้จากการแทนค่าตัวแปรลงในสมการการคำนวณมูลค่าของเงินในปัจจุบัน (Present value: PV) ได้ดังนี้
มูลค่าปัจจุบัน = มูลค่าในอนาคต / (1 + อัตราคิดลด)ระยะเวลา
PV = FV / [1 + (i/n)]n*t
เมื่อ FV = มูลค่าเงินในอนาคต
PV = มูลค่าปัจจุบัน
i = อัตราคิดลด (Discount rate)
n = จำนวนงวด
t = จำนวนระยะเวลา
ตัวอย่างที่ 3 ถ้าวางแผนจะเรียนต่อปริญญาโทในอีก 3 ปีข้างหน้า โดยต้องใช้เงินประมาณ 120,000 บาท จึงวางแผนนำเงินไปลงทุนซึ่งจะได้ผลตอบแทน 5% ต่อปี โดยจะสามารถเขียนเป็นเส้นเวลาได้ตามภาพเส้นเวลาด้านล่าง
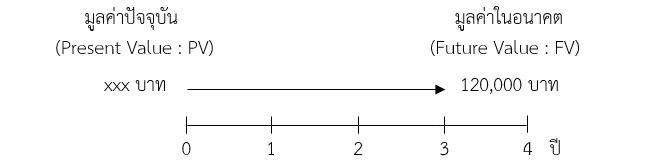
ดังนั้นจะต้องลงทุนด้วยเงินต้นเป็นจำนวนเงิน 120,000 / [1 + (0.05/1)]3*1 เท่ากับ 103,660.51 บาท ถึงจะได้เงิน 120,000 บาท ในอีก 3 ปีข้างหน้า ซึ่งสามารถแยกคำนวณทีละปีได้ดังนี้
ปีที่ 1; PV = 120,000.00 / (1 + 0.05)1 = 114,285.71 บาท
ปีที่ 2; PV = 114,285.71 / (1 + 0.05)1 = 108,843.54 บาท
ปีที่ 3; PV = 108,843.54 / (1 + 0.05)1 = 103,660.51 บาท
จะเห็นว่าต้องลงทุนวันนี้จำนวน 103,660.51 บาท และได้ผลตอบแทนอย่างน้อย 5% ต่อปี จึงจะมีเงิน 120,000 บาท ในอีก 3 ปีข้างหน้า แต่ถ้าเปลี่ยนใจจะเรียนปริญญาโทในอีก 2 ปี จะต้องเริ่มลงทุนด้วยเงิน 108,843.54 บาท หรือต้องใช้เงินเพิ่มขึ้นถึง 5,183.03 บาท เพราะระยะเวลาน้อยลง จึงต้องใช้เงินลงทุนเพิ่มขึ้น ดังนั้น การเริ่มต้นลงทุนยิ่งเร็วเท่าไหร่ ผลตอบแทนก็จะมีเวลาเติบโตมากขึ้นเท่านั้น
ตัวอย่างที่ 4 นางสาว กล้วยไม้ ต้องการมีเงิน 900,000 บาทในสิ้นปีที่ 4 เพื่อนําเงินไปลงทุนเปิดร้านค้าอาหาร โดยนางสาว กล้วยไม้ เลือกลงทุนด้วยการฝากเงินที่ให้ผลตอบแทน 7% ต่อปี โดยจะสามารถเขียนเป็นเส้นเวลาได้ตามภาพเส้นเวลาด้านล่าง
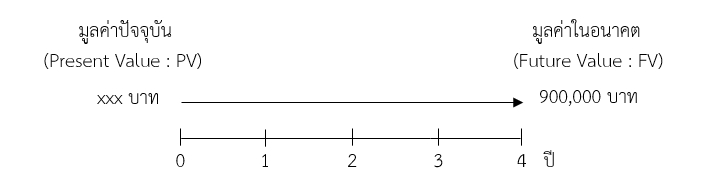
ดังนั้นจะต้องลงทุนด้วยเงินต้นเป็นจำนวนเงิน 900,000 / [1 + (0.07/1)]4*1 เท่ากับ 686,605.69 บาท ถึงจะได้เงิน 900,000 บาท ในอีก 4 ปีข้างหน้า ซึ่งสามารถแยกคำนวณทีละปีได้ดังนี้
ปีที่ 1; PV = 900,000.00 / (1 + 0.07)1 = 841,121.50 บาท
ปีที่ 2; PV = 841,121.50 / (1 + 0.07)1 = 786,094.85 บาท
ปีที่ 3; PV = 786,094.85 / (1 + 0.07)1 = 734,668.09 บาท
ปีที่ 4; PV = 734,668.09 / (1 + 0.07)1 = 686,605.69 บาท
จะเห็นว่าหากเปลี่ยนใจต้องการเปิดร้านค้าอาหารเร็วขึ้นจาก 4 ปี เป็น 2 ปี ก็จะต้องเริ่มลงทุนด้วยจำนวนเงินที่มากขึ้น จากเดิม 4 ปี ต้องใช้เงินลงทุนเท่ากับ 686,605.69 บาท เปลี่ยนเป็น 2 ปี ต้องใช้เงินลงทุนเท่ากับ 786,094.85 บาท แทน เนื่องจากถ้าระยะเวลายิ่งน้อยลงก็จะต้องใช้เงินลงทุนที่สูงขึ้น
ในการคำนวณมูลค่าปัจจุบันจะเรียกอัตราผลตอบแทน (Rate of return) ว่าเป็นอัตราคิดลด (Discount rate) เพราะมูลค่าปัจจุบัน (PV) จะมีค่าน้อยกว่ามูลค่าในอนาคต (FV) นั่นเอง ซึ่งจะเห็นได้ว่า โอกาสในการสร้างผลตอบแทนนั้นเกิดขึ้นจากระยะเวลา (อัจฉรา โยมสินธุ์, 2555) ดังนั้น แนวคิดเรื่องมูลค่าของเงินตามระยะเวลาจึงเป็นแนวคิดพื้นฐานที่ควรนำมาพิจารณาเสมอเมื่อมีการตัดสินใจทางการเงิน โดยเฉพาะการวางแผนการลงทุนและการวางแผนเพื่อการเกษียณ เพราะเป็นแผนการเงินที่ควรจะใช้ประโยชน์จากระยะเวลาในการสร้างผลตอบแทนให้เต็มที่
ประโยชน์ของมูลค่าของเงินตามระยะเวลา
มูลค่าของเงินตามระยะเวลา จัดเป็นการลงทุนในโครงการต่างๆ เงินทุนและผลตอบแทนจะเกิดขึ้นต่างเวลากัน ซึ่งถ้าเป็นลักษณะนี้แล้วจะนํามาเปรียบเทียบกันไม่ได้ เงินจ่ายลงทุนและผลตอบแทนที่ต่างเวลากันจะนํามาเปรียบเทียบกันได้ต้องทำให้ค่าอยู่ ณ เวลาเดียวกัน การที่จะทำให้อยู่ ณ เวลาเดียวกัน คือ ต้องคํานวณหามูลค่าอนาคต (Future value) หรือมูลค่าปัจจุบัน (Present value) แล้วแต่สภาวการณ์ (ธนาวัฒน์ สิริวัฒน์ธนกุล, 2564) โดยประโยชน์ของมูลค่าของเงินตามระยะเวลาแบ่งตามประเภทของมูลค่าของเงินตามระยะเวลา ดังนี้
1. มูลค่าในอนาคต (FV) เป็นเครื่องมือสำหรับคำนวณหาผลตอบแทนของเงินในการลงทุนที่ผลตอบแทนในปีแรกจะนำมาลงทุนต่อไปในปีที่สอง ทำให้เงินต้นในปีที่สองเท่ากับเงินต้นของปีที่หนึ่งบวกดอกเบี้ยของปีที่หนึ่ง และลงทุนต่อเนื่องไปเรื่อยๆ จนครบกำหนดการลงทุน (ดอกเบี้ยทบต้น) จะได้เงินรวมมาจำนวนหนึ่ง เช่น ถ้าเรานำเงินไปฝากธนาคาร 1000 บาท โดยจะได้รับอัตราดอกเบี้ย 4% ต่อปี เราก็สามารถคำนวนหาได้ว่าอีก 40 ปีข้างหน้าเราจะมีเงินเท่าไหร่ (ลิปปภาส พรสุขสว่าง, 2563)
2. มูลค่าปัจจุบัน (PV) เป็นเครื่องมือสำหรับการวางแผนการลงทุนในการลงทุนที่ให้ผลตอบแทนอย่างสม่ำเสมอ เพื่อวางแผนว่าถ้าหากต้องการเงินจำนวนหนึ่งในอนาคตคุณจะต้องมีเงินลงทุนเริ่มต้นเท่าไหร่ (K. Pair, 2561) ซึ่งจะทำให้ทราบว่าหากได้รับสัญญาว่าจะได้เงินคืน 1 บาทในอีก 5 ปีข้างหน้า เงินใน 5 ปีข้างหน้าย่อมมีค่าน้อยกว่าเงินที่มีในปัจจุบัน เนื่องจากการที่เราลงทุนในวันนี้ทำให้เรามีเงินมากขึ้นในอีก 5 ปีข้างหน้า หรือทำให้สามารถหามูลค่าของตราสารทางการเงินเทียบเป็นอัตราปัจจุบันในขณะที่อัตราดอกเบี้ยคงที่ หรือทำให้สามารถเปรียบเทียบผลตอบแทนของตราสารทางการเงินที่มีระยะชำระคืนไม่ตรงกัน
สรุป
มูลค่าของเงินตามระยะเวลา (Time value of money: TVM) เป็นแนวคิดเกี่ยวกับมูลค่าของเงินตามระยะเวลา โดยเงินที่ได้รับในวันนี้มีมูลค่าน้อยกว่าเงินที่จะได้รับในอนาคต เพราะสามารถสร้างผลตอบแทนได้จากเงินที่ได้รับในวันนี้ ซึ่งสามารถแบ่งประเภทของมูลค่าของเงินตามระยะเวลาออกได้เป็น 2 ประเภท ได้แก่ (1) มูลค่าในอนาคต (Future Value) คือ จำนวนเงินในอนาคตที่เกิดจากการเพิ่มขึ้นของมูลค่าเงินทุนในระยะเวลาหนึ่งด้วยดอกเบี้ยทบต้น (Compound interest rate) และ (2) มูลค่าปัจจุบัน (Present value) คือ จำนวนเงินในอนาคตที่ถูกปรับลดด้วยอัตราคิดลด (Discount rate) เพื่อแปลงกลับเป็นมูลค่าปัจจุบัน
ประโยชน์และความจำเป็นของมูลค่าของเงินตามระยะเวลา โดยแบ่งตามประเภทของมูลค่าของเงินตามระยะเวลาได้ว่า มูลค่าในอนาคตจะบอกให้ทราบว่าการลงทุนในวันนี้จะมีผลตอบแทนเท่าไหร่ในอนาคต ในขณะที่มูลค่าปัจจุบันจะทำให้รู้ว่าผลตอบแทนในอนาคตมีมูลค่าเท่าไหร่ในปัจจุบัน โดยที่อัตราดอกเบี้ยสูงมูลค่าในอนาคตก็จะสูงไปด้วย ในขณะที่ถ้าอัตราดอกเบี้ยสูงจะทำให้มูลค่าปัจจุบันต่ำ เพื่อนำไปสู่การตัดสินใจทางการเงินได้อย่างเหมาะสม และเป็นประโยชน์ต่อผู้มีส่วนเกี่ยวข้องทั้งทางตรงและทางอ้อม
ข้อเสนอแนะ
การเลือกใช้เครื่องมือหรือเทคนิคต้องเลือกให้สอดคล้องและเหมาะสมกับข้อมูลที่จะนำไปพิจารณาการลงทุน เช่น ระยะเวลาคืนทุน มูลค่าปัจจุบันสุทธิ อัตราผลตอบแทนภายใน และอัตราส่วนผลตอบแทนต่อต้นทุน เป็นต้น ดังนั้นการนำเครื่องมือหรือเทคนิคไปใช้ในการประเมินเพื่อพิจารณาตัดสินใจลงทุนควรต้องศึกษาข้อมูลที่เกี่ยวข้องประกอบการตัดสินใจให้มากที่สุดเพื่อสามารถได้ข้อสรุปซึ่งจะนำไปสู่การตัดสินใจที่เป็นประโยชน์สูงสุดแก่นักลงทุน นักวิเคราะห์ทางการเงิน ผู้บริหารองค์กร และผู้ที่มีความสนใจให้ได้มากที่สุด
บรรณานุกรม
ไทยพับลิก้า. (2561). “มูลค่าเงินตามเวลา” Time Value of Money หลักการช่วยตัดสินใจลงทุน. สืบค้นเมื่อ 28 กรกฎาคม 2564, จากเว็บไซต์: https://thaipublica.org/2018/03/kkp-financial-literacy-07/
ธนาคารแห่งประเทศไทย. (2557). เงินเฟ้อ. สืบค้นเมื่อ 28 กรกฎาคม 2564, จากเว็บไซต์: https://www.bot.or.th/App/FinancialLiteracy/ExchangeRate/01_01_contentdownload_inflation.pdf
ธนาวัฒน์ สิริวัฒน์ธนกุล. (2564). มูลค่าเงินตามเวลา time value of money. สืบค้นเมื่อ 28 กรกฎาคม 2564, จากเว็บไซต์: https://allaboutfin.com/fin-principle/มูลค่าเงินตามเวลา-time-value-of-money
ลิปปภาส พรสุขสว่าง. (2563). ความเข้าใจเกี่ยวกับอัตราดอกเบี้ย. สืบค้นเมื่อ 28 กรกฎาคม 2564, จากเว็บไซต์: https://www.econ.cmu.ac.th/econadmin/files/Future%20Value,%20Present %20Value,%20and%20Interest%20Rates%5B1%5D.ppt
ศิรประภา ศรีวิโรจน์, ลักขณา ลุสวัสดิ์ และ ธตรฐ จำรูญกุล. (2563). การประเมินโครงการลงทุนด้วยเครื่องมือวิเคราะห์ทางเศรษฐศาสตร์. วารสารวิชาการมหาวิทยาลัยอีสเทิร์นเอเชีย, 10(3), 21-30.
อรุณรุ่ง วงศ์กังวาน. (2557). มูลค่าปัจจุบัน (Present value). สืบค้นเมื่อ 28 กรกฎาคม 2564, จากเว็บไซต์: http://www.elfms.ssru.ac.th/arunroong_wo/file.php/1/2559-2/2/unit3.pdf
อัจฉรา โยมสินธุ์. (2555). 365+1...คำศัพท์การเงินและการลงทุน (พิมพ์ครั้งที่ 1). กรุงเทพฯ: บริษัท บุญศิริการพิมพ์ จำกัด.
K. Pair. (2561). Present Value คืออะไร? ตัวเลข PV คือ ค่าที่บอกอะไร. สืบค้นเมื่อ 28 กรกฎาคม 2564, จากเว็บไซต์: https://greedisgoods.com/present-value-คือ-pv-คือ/
MONEY BUFFALO. (2563). Time Value of Money คืออะไร. สืบค้นเมื่อ 28 กรกฎาคม 2564, จากเว็บไซต์: https://www.moneybuffalo.in.th/vocabulary/time-value-of-money-%E0%B8 %84%E0%B8%B7%E0%B8%AD%E0%B8%AD%E0%B8%B0%E0%B9%84%E0%B8%A3
myAccount. (2561). PRESENT VALUE (มูลค่าปัจจุบัน). สืบค้นเมื่อ 28 กรกฎาคม 2564, จากเว็บไซต์: https://www.myaccount-cloud.com/Article/Detail/91499
PeerPower. (2562). Time Value of money คืออะไร ทำไม SME ควรศึกษา. สืบค้นเมื่อ 28 กรกฎาคม 2564, จากเว็บไซต์: https://www.peerpower.co.th/blog/smes/busmgt/start-bus/time-value-of-money/
Sarker, B.R. และ Pan, H. (1994). Effects of inflation and the time value of money on order quantity and allowable shortage. International Journal of Production Economics, 34(1), 65-72.

